ポールウオーキング(以下、PW)とノルディックウオーキング(以下、NW)は、共に2本のポールを用いる歩行メソッドですが、開発された経緯や歩行技術は異なり、ポールの果たす役割も異なっています。一方、健康づくりの手軽なウオーキングを実践する高齢者も多く、両メソッドを楽しむ方、年をとってもNWという方もいれば、足腰が弱くなったのでNWからPWに変えたという方もいます。PWとNWが、健康づくりの場やあるいは歩行のリハビリの場で、競合、相互依存している関係を、ロトカ・ヴォルテラ方程式で表される抽象的な数理モデルを用いて分析します。
1.ロトカ・ヴォルテラ・モデル(以下、LVモデル)
1ー1)仮定と定義
(仮定1)PW とNWは競合している。
モデルでは、PWとNWの関係は、競争的であると仮定します。
即ち、PWにとって、NWが活況であることは、PWへの需要を減少させ、逆に、PWが活況であると、NWへの需要は減少すると、まずは仮定します。
t期にPWの新たに愛好者となった人数を x1(t)、NWの新たに愛好者となった人数を x2(t)で表します(添え字の i=1 はPWを表し、i=2 はNWを表します(以下、同様です))。
(仮定2)企業行動については、次の3つを仮定します。
(仮定2ー1)PW、NW共に、普及を図る企業家はプライス・テイカーとし、t期のPWとNWの市場価格は次のように決定されると仮定します。
p1(t) = α1-β11×1(t) -β12×2(t) (1)
p2(t) = α2-β21×1(t) -β22×2(t) (2)
x1(t)はt期にPWの新たに愛好者となった人数、x2(t)はNWの新たに愛好者となった人数、α1、α2は各々PWとNWの内在的な魅力度を表すパラメータ、βiiはiの市場における飽和率(限界効用逓減の率とも言える)、βijはiに対するjの競争力を示すパラメータです。
(1)、(2)式は、競合相手の新規愛好者数の影響をシフト項目に持つ、PW、NWの右下がりの需要関数と見ることもできます。
(仮定2-2)PW、NW共に、他方の新規愛好者数を与件として、収益最大化を図るように自身の新規愛好者数を決定すると仮定します。簡単化のために、PW、NW共に、費用関数は線型と仮定し、iの費用をCi = mi×xiとします。ここで、mi>0はiの限界費用であり、平均費用でもあります。この時、企業家iの収益(πi = pixi-Ci)は、
πi(t)= (αi-βiixi(t) -βijxj(t))xi(t)-mixi(t) (3)
と書き表せます。
収益最大化の条件は、xiの限界収益がゼロに等しくなることなので、(3)式のxiについての偏微分
∂πi /∂xi = (αi-mi)-2βiixi(t)-βijxj(t) (4)
がゼロになります。PW、NWの双方について(4)式がゼロになるとき、双方の収益は最大化されており、この状態を経済学では「ナッシュ均衡」と言います。
(仮定2-3)ナッシュ均衡でない過渡的な状態での数量調整のメカニズムは、限界収益の正負によって、数量を増減すると仮定します。
即ち、
∂πi /∂xi > 0 => dxi(t)/dt > 0
∂πi /∂xi < 0 => dxi(t)/dt < 0 (5)
更に、そのxi(t)の「変化率」を限界収益に比例するように決めると仮定します。
従って、過渡的な調整式は、次式で表せます。
dxi(t)/dt = (∂πi /∂xi)xi(t) , i=1,2 (6)
ただし、ここで比例定数は1としています。
限界収益は、(4)式であらわされるので、(6)式は、次のように書き直せます。
dxi(t)/dt = ((αi-mi)-2βiixi(t)-βijxj(t))xi(t) (7)
(7)式で表される微分方程式を「一般化ロトカ・ヴォルテラ方程式」と言います。
1-2)「動き」の可視化:位相空間
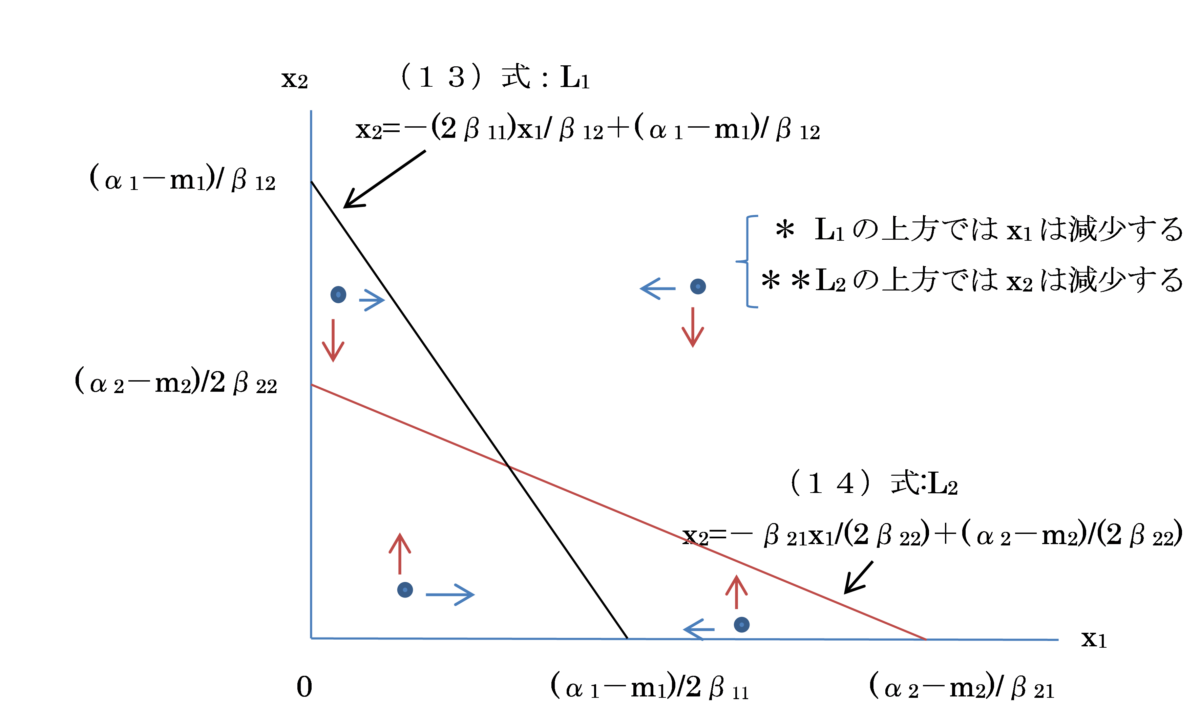
任意のt時点での(7)式の連立方程式の解(x1(t)、x2(t))が、どの方向に動くのかは、横軸:x1(t)、縦軸:x2(t)とする2次元座標「位相図」を使って表すことができます。
まず、x1(t)が動かなくなる条件、即ち、dx1(t)/dt = 0となる条件は、(7)式から
(α1-m1)-2β11×1(t)-β12×2(t)=0 (8)
または、
x1(t) = 0
となるときです。
同様に、x2(t)が動かなくなる条件、dx2(t) = 0となるのは、
(α2-m2)-2β22×2(t)-β21×1(t)=0 (9)
または、
x2(t) = 0
のときです。
式(8)と(9)は、x1(t)、x2(t)座標上では、直線L1、L2として表すことができます。
(x1(t) = 0、x2(t) = 0)の点は原点になります。
式(8)と(9)をアイソクラインと呼びます。L1とL2の交点(無論、交点がない場合もある)では、点(x1*,x2*)はどの方向へも動かなくなります。こうした点を定常点と呼びます。この点では、(8)と(9)が同時に成立しているので、(仮定2-2)のところで述べたように「ナッシュ均衡」になっています。また、定常点ではない点が時間と共に定常点に近づくとき、その定常点を安定と言い、逆に時間の経過と共に遠ざかるとき不安定と言います。
1-3)5つの基本形
(8)と(9)の2つのアイソクラインを示す直線がx1とx2座標上に描く図形には5つの基本形があり、点(x1、x2)が描く軌跡群にもそれぞれ特徴が生じています。
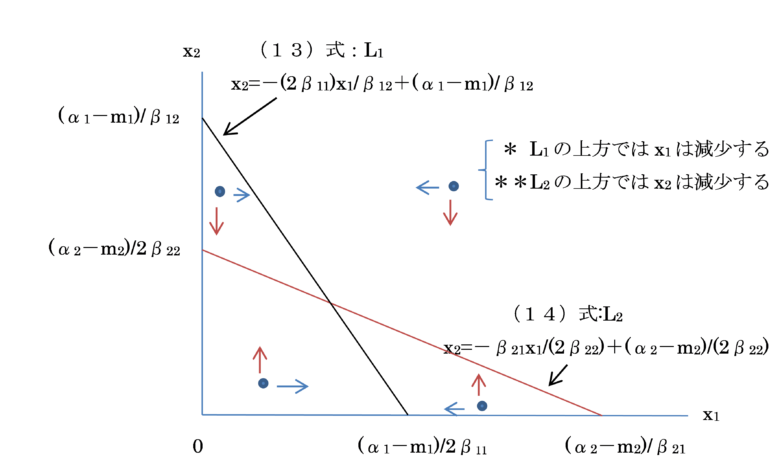
・基本形A:β12=β21=0のとき。
PW、NWは、それぞれが独占する市場において、他方が選択する戦略とは独立に、最適な新規愛好者数を選択できる。しかも、2つのアイソクラインが交わる交点は、双方が最適選択が実現された「安定な共存解」となっています。
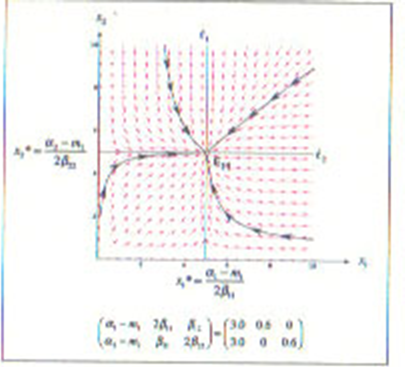
・基本形B:2(α2-m2)β11/(α1-m1)>β21>0 &
2(α1-m1)β22/(α2-m2)>β12>0 のとき
PW、NWは市場を介して相手方に影響を及ぼしているが(β21>0、β12>0)、その影響度合いは、ともに一定の制限が加えられる状況です。
2本のアイソクラインの交点も「安定な共存解」となっています。
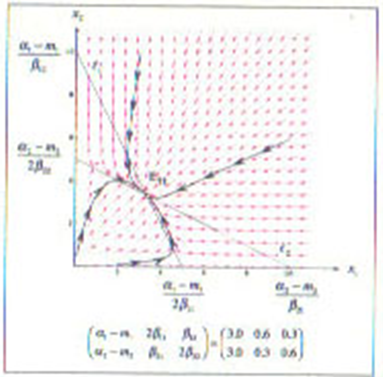
・基本形C:β21>2(α2-m2)β11/(α1-m1)>0 &
2(α1-m1)β22/(α2-m2)>β12>0 のとき
NWが市場を介してPWに与える影響(β12>0)が微小であるのに対し、PWがNWに対して及ぼす影響(β21>0)が大きく、閾値2(α2-m2)β11/(α1-m1)を超える場合です。
アイソクラインは交わらず、従って、共存解は存在しません。安定となる均衡点は図中X1軸上のE10であり、そこでは、市場において相対的に優越するPWが生き残り、NWは市場から淘汰されてしまいます。
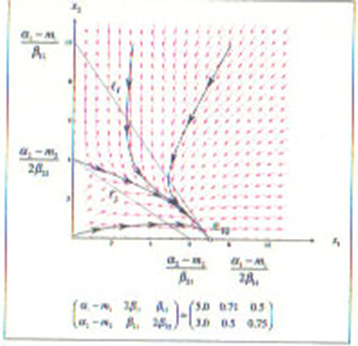
・基本形D:2(α2-m2)β11/(α1-m1)>β21>0 &
β12>2(α1-m1)β22/(α2-m2)>0 のとき
基本形Cとはちょうど逆の関係が成立する状況です。PWが市場を介してNWに与える影響(β21>0)が微小であるのに対し、NWがPWに対して及ぼす影響(β12>0)が大きく、閾値2(α1-m1)β22/(α2-m2)を超える場合です。
アイソクラインは交わらず、従って、共存解は存在しません。安定となる均衡点は図中X2軸上のE01であり、そこでは、市場において相対的に優越するNWが生き残り、PWは市場から淘汰されてしまいます。
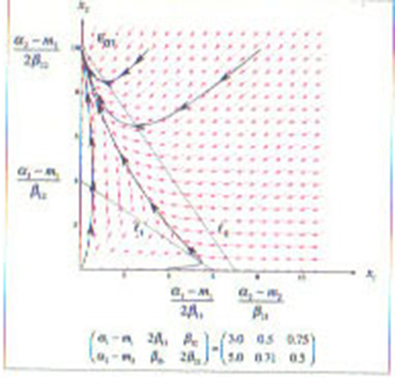
・基本形E:β21>2(α2-m2)β11/(α1-m1)>0 &
β12>2(α1-m1)β22/(α2-m2)>0 のとき
PW、NW共に、市場を介して他方に与える影響(β21、β12)が、所定の閾値を超える状況です。
2本のアイソクラインは交点を持ち、従って、共存解E11は存在するが、この均衡点は不安定です。安定な2つの均衡点が存在し、点E10、E01です。このようなケースを「双安定」な状況と言いますが、極めて希な場合を除いては、両者が実際の市場で共存することはできません。どちらが残るかは、初期状態の違いによって、長期的局面での存続と消滅のいずれかになります。
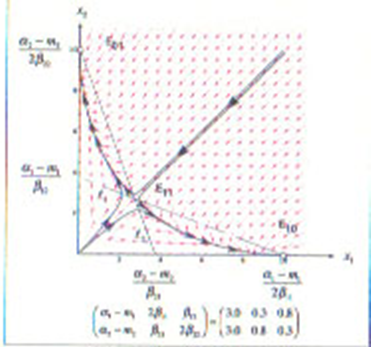
以上をまとめると、「PWとNWとが市場を介して競合、相互依存する時には、各々の企業が自己の限界収益の正負に応じて、新規愛好者数の獲得を比例的に調整するという極めて当然と思われる行動を取っていたとしても、8個のパラメータの大小関係で規定される運動法則によって、場合によっては共存したり、一人勝ちしたり、市場から退出を余儀なくされる。」ということです。
2.競争戦略
LVモデルによれば、NWと競合する地域でPWの普及を意図する企業家は、8個のパラメータを、イノベーションや経営革新によって、自己に有利な運動法則が働くようにすることが肝要となります。
NWが先行普及している地域や国々への市場参入、成長、そして発展期での競争戦略の要点と、競争に敗れ市場からの撤退を迫られた時の生き残り策、すなわち、LVモデルに基づく競争戦略のシナリオを考えてみます。
2-1)市場参入時:棲み分け
NWに対しては出遅れているので、まずは、NWと真向から対立する領域に攻め込むのではなく、「NWの影響を受け難くPWに高い価値を認める人々」の獲得を図り、「NWとの棲み分けを図る」べきでしょう。即ち、先のパラメータを使って表現すれば、限界効用が高く(α1>α2)、且つ限界効用が逓減していない(β11<β22)人達へのアプローチです。併せて、限界コストm1が相対的に高くならないようにコスト管理できれば(m1<m2)、基本形Aのグラフから、PWの相対シェアはNWよりも大きな均衡状態を運動法則の結果として実現し得ることが分かります。広報戦略は、このような人々へPWならでは魅力を伝えることがまずは主眼になります。
目指すべきは、
(α1-m1)/(2β11)>(α2-m2)/(2β22) (10)
とすることです。
2-2)成長期:共存
PWの拡大に伴い、否応なしにNWとの競合が発生します。潜在的な愛好者獲得の鍵となる有能で市場動向に敏感な指導コーチの取り合いが現出すると予想します。NWからの影響度合い(β12)を低め、PWの限界効用(α1)を高め、限界費用(m1)を抑制することが必要です。普及のための組織・体制を作り、PWを主体とする種々のニーズに応える多様なプログラムの開発や、広くPWの効能を潜在的な愛好者に訴えると伴に、PW指導コーチになることがNWのそれよりもビジネス的にも社会的にも魅力的であることを伝えることが重要になると思います。
そして、
(α1-m1)/(β12)>(α2-m2)/(2β22) (11)
を実現できれば、基本形Bのグラフが示すように、NWとの共存が可能となります。
2-3)発展期:メジャー化
次なる飛躍は、市場の大半を獲得するメジャーへの挑戦です。このための要件は、(11)式に加えて、NWに及ぼす影響度合い(β21)を強めることです。例えば、PWのある生活を、より豊かでより楽しいものにすることではないでしょうか。誰でもがPWに触れる機会や場所を広め、更に、NWならではの魅力をも凌駕できる仕組みが創造できればベストです。
そして、
(α1-m1)/(2β11)>(α2-m2)/(β21) (12)
を実現できれば、基本形Cのグラフが示すように、NWを市場から排除することも可能になってきます。
2-4)生き残り戦略
最後に、努力の甲斐なくNWとの競争に敗れ市場からの撤退を迫られた場合(基本形D)の「生き残り策」についてです。具体的には、NWが攻め込んでこられない固定的顧客に支えてもらうことです。この戦略を図で表現すると、固定客(x1*で示される)のところで直線L1が垂直になるようにすることです(垂直線は、dx1/dt = 0を意味しています)。例えば、PWが歩行リハビリの唯一のウォーキング方法として、広く認められたような場合が考えられます。
3.競争の指標
LVモデルに基づく競争戦略の指標は、市場のシェアとなります。
LVモデルの位相図上の点と原点を結んだ直線の傾き(X2/X1)はX2の伸び率よりX1の伸び率が大きいとき小さくなり、逆の時には大きくなります。すなわち、PW(X1)とNW(X2)の新規愛好者の獲得動向は、この直線の傾きの動向で判断することができます。
PWの市場のシェアS1はX1/(X1+X2)です。この分母と分子をX1で割ると、S1=1/(1+X2/X1)と変形できます。シェアは直線の傾きのみの関数となり、傾きが小さくなれば大きくなり、傾きが大きくなれば小さくなります。
すなわち、PWがNWより新規愛好者の獲得が増えていれば、直線の傾きは小さくなり、シェアは大きくなります。逆に、直線の傾きが大きくなる時は、シェアが下がっているときです。
LVモデルによる競争シナリオが順調に推移している場合は、この直線の傾きは一貫して小さくなっています。
作成者:峯岸 瑛(みねぎし あきら)
作成日:2022年11月25日
文献
1.藤垣芳文:成蹊大学・経済学部(2014年後期)「経済動学と力学系の理論」の講義資料