月: 2022年12月

『ポールの先端を振り出した足の踵辺りに置く』のは何故か？
～ポールウォーキングのエネルギー転換は、効率が良い～

日本ポールウォーキング協会 専務理事　峯岸 瑛（みねぎし あきら）

１．ベクトルとは？
ベクトルとは、向きと大きさを持つ量のことで、通常は、矢印の付いた線分（これを「有向線分」と言います）で表されます。矢印が向きを意味し、線分の長さが大きさを意味します。

始点 A を、通常では、原点（０，０）に取ります。この時、２次元ベクトルＡＢは、終点Ｂのx座標とｙ座標を使って、ベクトル AB＝（ｘ、ｙ）のような形で表現されます。これを、ベクトルの成分表示と言います。また、ベクトル AB の大きさは、三角形の斜辺の公式から、以下のようになります。
ベクトル AB の大きさ＝（xの2乗 + yの2乗）の平方根

さて、ベクトルは、足し合わせることができます。
２つのベクトル AB＝(x1,y1)と、CD＝(x2,y2)を足し合わせたベクトル EF は、成分表示をすれば、(x1+x2,y1+y2)と表記でき、大きさは、(( x1+x2)2 乗+ (y1 + y2)2 乗)の平方根 となります。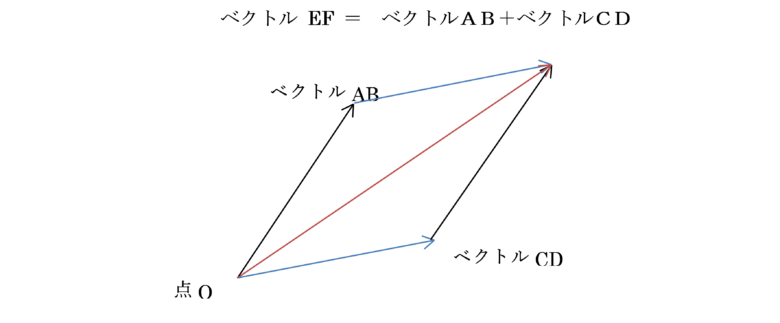例えば、ベクトル AB＝(x,y)は、ベクトル OA＝(x,0)と OB＝(0,y)が足し合わさったものです。

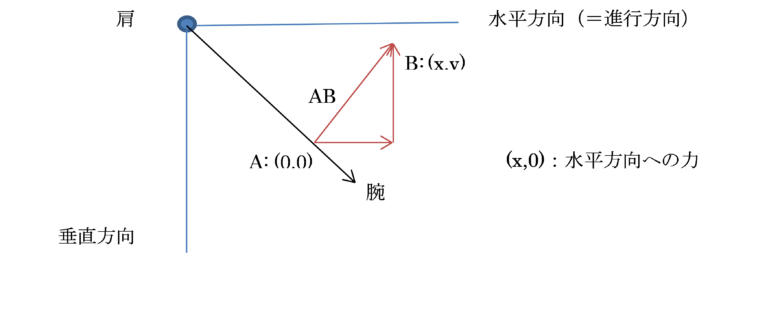
（例）肩を支点に、腕を伸ばしたまま振り上げた場合の進行方向への力の大きさは、振り上げる力をベクトル AB＝(x,y)で表すとすると、x です。ここで x 方向は水平方向（＝進行方向）で、y 方向は垂直方向を意味しています。

２．ポールの先端を振り出した足の踵辺りに置く意味は？
振り出した左足（＝立脚）の接地点を A、反対の右手に持つポールの接地点を B とすると、左足の踵が接地し（従って両脚が地面に接地している）、ポールの先端も地面に接地している時は、以下の図のように、その瞬間を表すことができます（３点支持）。

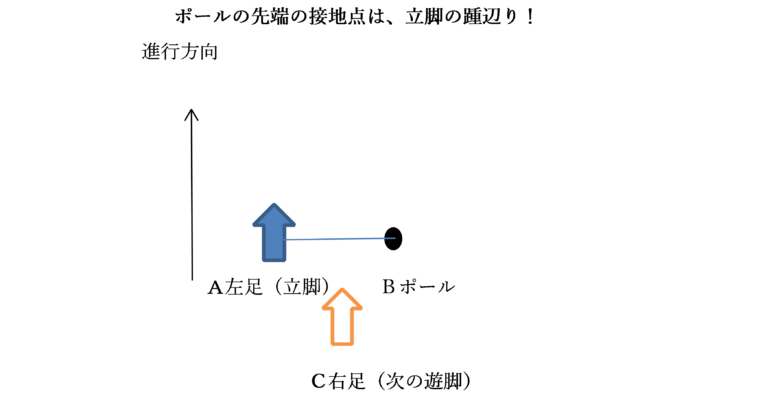
人間の直立二足歩行は、位置エネルギーを運動エネルギーに変えることで、可能になると考えられます（倒立振子モデル）。上の図を使って説明すると、次に遊脚となる右足を挙げた瞬間は、体重を支える支持基底面が線分 AB になります。この瞬間は、身体は、左右には倒れにくく、前後には倒れ易い状態になっています。

ここで、直立時の位置エネルギーを運動エネルギーに変わる原理の理解のために、身体を進行方向（図の CD の方向）に倒してみましょう。図の長方形が身体を表しています。また、線分 AB と直線 CD の交点を O、角度をαとします。

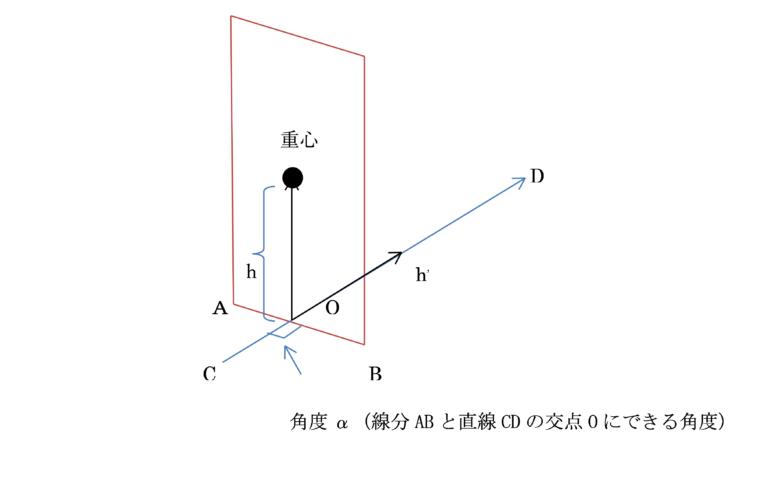
倒れた後では、身体の重心（図中の●）は、高さ分（ここでは h）の距離だけ、交点 O から前方方向に移動します（ここで、h’を倒れた時の重心の進行方向の距離とします）。

さて、問題です。倒れた時の重心の「交点 O（線分 AB と直線 CD の交点）から進行方向への成分（即ち h’）」がもっとも大きくなる角度αは、何度でしょうか？
答えは、直角の９０度です。倒れた時の重心は、角度αが直角でないと、直線 CD（進行方向）から左右のいずれかにズレ（下図のγです）てしまいます。そのため、進行方向の大きさは、h ではなく、それより小さい（図ではβほど小さくなっています：h-β）。また、このズレは、直立二足歩行について言えば、左右への重心の移動を意味しています。

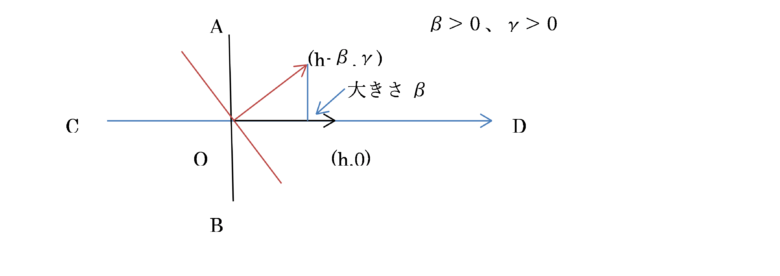
角度αが直角となる状態は、ポールの先端の接地点が立脚の踵の辺りに置かれた状態です。即ち、身体が倒れる時間を仮に１単位とすれば、進行方向にもっとも距離が大きいことの意味は、進行方向への単位当たりの速度がもっとも速いことを意味していますし、左右への重心のブレが生じないことの意味は、歩行の左右への安定性を崩す力が生じていないことを意味しています。

（注）NPWA会報誌Vol.16（２０１８年８月３１日）に寄稿したものを、一部修正、加筆しました（２０２２年１１月３０日）。